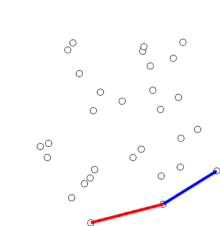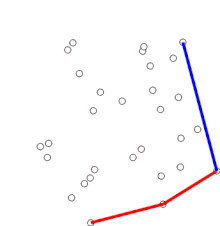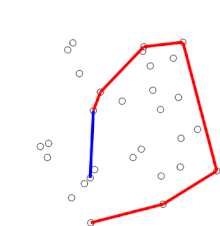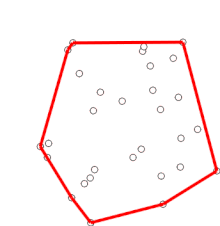
Clasificación De Los Vectores
Los vectores se clasifican en libres, deslizantes, fijos, unitarios, concurrentes, opuestos, colineales, paralelos, coplanares, esta es la clasificación más generalizada que reconocen las matemáticas como ciencia exacta y que de forma primaria estudia estos elementos de medición, sobre un espacio abstracto en el cual se establecen las medidas entre un punto y otro.
Clasificación de los Vectores.
Libres.
Son aquellos que se emplean para la medición genérica de espacios, los cuales no requieren de una medida determinada pues los mismos aplican para diversas situaciones; de aquí que los vectores libres sean útiles para la representación espacial indefinida.
Deslizantes.
Considerados así porque en el cálculo de las direcciones estos pueden realizar movimientos determinados en grados, sin que los mismos cambien en su medida o longitud.
Fijos.
Es aquel que se establece para una medida determinada, que solo funciona para el cálculo de la distancia que pueda establecerse entre dos extremos de un segmento, de modo tal que los vectores fijos solo se emplean para el cálculo de una determinada función.
Unitarios.
En este momento definimos un vector unitario como aquel que su medida de expresión es igual a 1
Concurrentes.
Son aquellos que parten de un solo extremo, es decir, su dirección vectorial son aquellos que parten de un mismo punto, los cuales establecen diferentes longitudes.
Opuestos.
Son aquellos que presentan la misma longitud, pero diferente dirección con la finalidad de que se puedan establecer medidas vectoriales diversas; en su representación gráfica estos vectores permiten establecer coordenadas opuestas.
Colineales.
Son aquellos vectores que presentan la misma dirección como por igual la misma longitud, siendo determinante el hecho de que se presenta de forma subseguida en la gráfica.
Paralelos.
Estamos ante vectores que de una forma u otra se presentan con igual longitud y dirección pero como su nombre bien lo indica se tratan de vectores que se presentan en el plano con una cierta distancia pero uno al lado del otro.
Coplanarios.
Se tratan de vectores, que se encuentran distribuidos de una forma u otra en el mismo espacio vectorial, pero que no parten del mismo punto ni encuentran direcciones iguales.